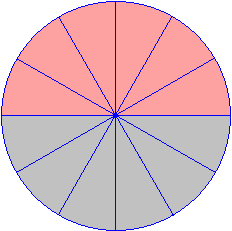
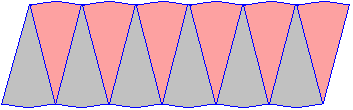
 Area of a Circle Equipment: You will need a compass, pair of scissors, ruler and protractor for this activity. Purpose: To discover a formula for the area of a circle. Step 1: Using the compass, draw a circle of radius 7 cm. Then mark the circle's centre and draw its radius. Step 2: Place the centre of the protractor at the centre of the circle and the zero line along the radius. Then mark every 30º around the circle. Step 3: Using a ruler and a pencil, draw lines joining each 30º mark to the centre of the circle to form 6 diameters. The diagram thus obtained will have 12 parts as shown below. Step 4: Colour the parts as shown below. Step 5: Cut out the circle and then cut along the diameters so that all parts (i.e. sectors) are separated. Step 6: Arrange all of the sectors to make a shape that approximates a parallelogram as shown below. Step 7: Using a ruler, measure the base and the height of the approximate parallelogram obtained in Step 6. Questions:1. Calculate the area of the figure in Step 6 by using the formula: 2. What is the area of the circle drawn in Step 1? 3. It appears that there is a formula for calculating the area of a circle. Can you discover it? Formula for the Area of a Circle From the above activity, it is clear that by arranging the sectors of the circle as a parallelogram that: Remember:The area, A, of a circle is given by the following formula where r is the radius of the circle: Example 8 Solution: So, the area is 616 m2. Note:To find the area of a region enclosed within a plane figure, draw a diagram and write an appropriate formula. Then substitute the given values and use a calculator, if necessary, to obtain the required area. Example 9Find the area of a circle of whose diameter is 11 cm using π = 3.14. Round your answer to 2 decimal places. Solution: So, the area is 94.99 cm2. Numbers, numbers everywhere , There seems to be so many different types That I can’t get them all clear! Today we are detectives on case to find out more about numbers. You will be given the worksheet that is in the file below to complete based on types of numbers.
 Use the links below to assist you with your mission. LINKS Triangles A triangle has three sides and three angles The three angles always add to 180°Equilateral, Isosceles and Scalene There are three special names given to triangles that tell how many sides (or angles) are equal. There can be 3, 2 or no equal sides/angles: Equilateral TriangleThree equal sides Three equal angles, always 60° Isosceles TriangleTwo equal sides Two equal angles Scalene TriangleNo equal sides No equal angles What Type of Angle? Triangles can also have names that tell you what type of angle is inside: Acute TriangleAll angles are less than 90° Right TriangleHas a right angle (90°) Obtuse TriangleHas an angle more than 90° |
ThoughtBe the best version of yourself possible. Archives
January 2014
Categories |
||||||




 RSS Feed
RSS Feed
